Relación entre función y ecuación de segundo grado.

Relación entre función y ecuación de segundo grado.

Una ecuación de segundo grado o ecuación cuadrática de una indeterminada ​es una ecuación que tiene la forma de una suma algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un polinomio de segundo grado o polinomio cuadrático. La expresión canónica general de una ecuación cuadrática de una variable es:

Donde x es la variable, y a, b y c constantes; a es el coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. Este polinomio se puede interpretar mediante la gráfica de una función cuadrática, es decir, por una parábola. Esta representación gráfica es útil, porque las intersecciones o punto tangencial de esta gráfica, en el caso de existir, con el eje X coinciden con las soluciones reales de la ecuación.

  

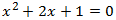
El discriminante de la ecuación es

$$\Delta =b^2-4ac=$$

$$=2^2-4\cdot 1\cdot 1=$$

$$=4-4=0$$

Por tanto, la ecuación tiene una solución real doble.

Aplicamos la fórmula: 

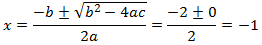
Luego la solución doble es x = -1.

Una factorización de la ecuación es 

(x+1)2=0 Para representar una función de segundo grado, necesitas saber qué forma va a tener la función para poder encontrar los puntos clave que te determinarán el trazado de la función¿Cuáles son esos puntos y como se obtienen? Las funciones de segundo grado tienen forma de parábola, que puede ir con el vértice hacia arriba: 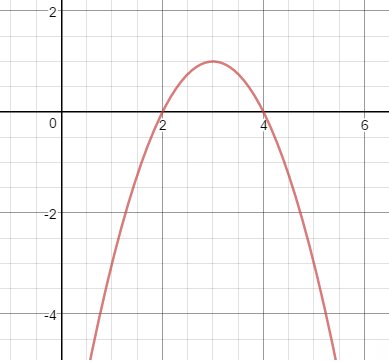O con el vértice hacia abajo: Que la parábola esté con el vértice hacia arriba o hacia abajo dependerá de los signos del coeficiente “a” de la función de segundo grado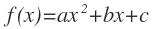Cualquier función de segundo grado, ya sea completa o incompleta, va a tener forma de parábola. Será distinta en cada caso (más abierta, menos abierta, con el vértice situado en un puno diferente…) pero siempre será una parábola.

Para representar una función en los ejes de coordenadas necesitas realizar una tabla de valores y hallar una serie de puntos, para que al unirlos después, podamos representar esa función. Esos puntos se obtienen, eligiendo valores de x y calculando los valores de “y” que les corresponden (si no sabes bien como hacerlo, en el ejemplo de más abajo te lo explico). En el caso de las funciones de segundo grado, no podemos elegir cualquier valor de x para obtener los puntos que definan la función, ya que nos encontraríamos perdidos y no sabríamos la forma exacta de la parábola. Hay que calcular los puntos de la parábola siguiendo un criterio, que nos permitan después dibujar la parábola al unirlos. Por eso, el primer punto que necesitamos es el vértice de la parábola. Una vez tenemos ese punto, podemos darle dos o tres valores de x a la derecha del vértice y calcular el valor de y, con lo que tendríamos dos o tres puntos más a la derecha del vértice y hacer lo mismo por la izquierda. Finalmente tendremos unos 5 o 7 puntos que definirán la parábola que estamos buscando perfectamente.

https://www.youtube.com/watch?v=OqoQzn6PjW4